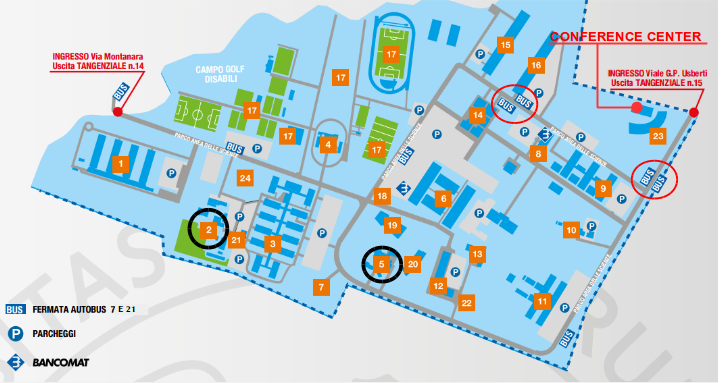
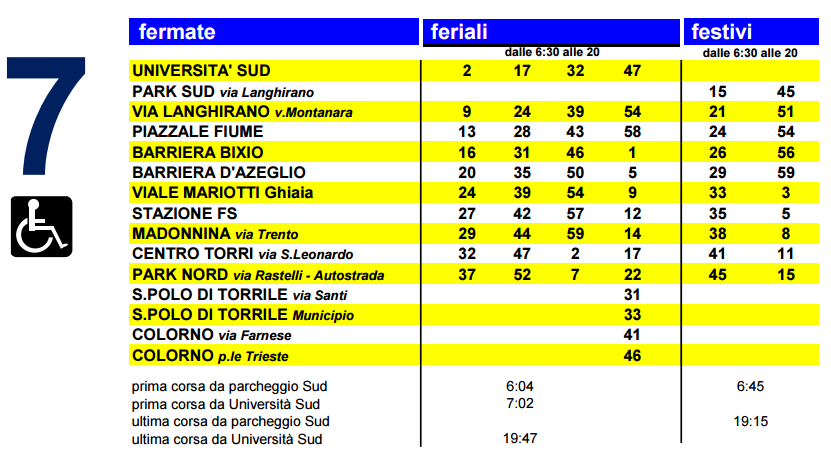
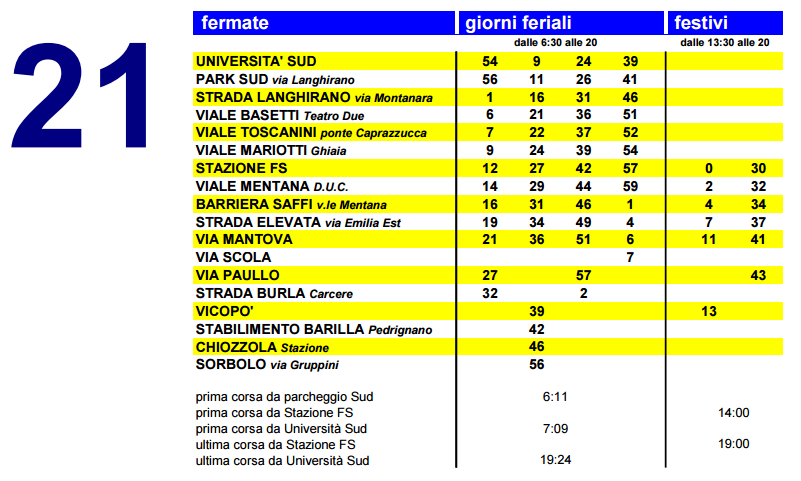
| 9:30 - 9:50 | Andrea Mazzolini - ICTP, Trieste
Zipf and Heaps laws from dependency structures in component systems 
Complex natural and technological systems can be considered, on a coarse-grained level, as assemblies of elementary components: for example, genomes as sets of genes, or texts as sets of words. On one hand, the joint occurrence of components emerges from architectural and specific constraints in such systems. On the other hand, general regularities may unify different systems, such as the broadly studied Zipf and Heaps laws, respectively concerning the distribution of component frequencies and their number as a function of system size. Dependency structures (i.e., directed networks encoding the dependency relations between the components in a system) were proposed recently as a possible organizing principles underlying some of the regularities observed. However, the consequences of this assumption were explored only in binary component systems, where solely the presence or absence of components is considered, and multiple copies of the same component are not allowed. Here, we consider a simple model that generates, from a given ensemble of dependency structures, a statistical ensemble of sets of components, allowing for components to appear with any multiplicity. Our model is a minimal extension that is memoryless, and therefore accessible to analytical calculations. A mean-field analytical approach (analogous to the "Zipfian ensemble" in the linguistics literature) captures the relevant laws describing the component statistics as we show by comparison with numerical computations. In particular, we recover a power-law Zipf rank plot, with a set of core components, and a Heaps law displaying three consecutive regimes (linear, sub-linear and saturating) that we characterize quantitatively.
|
| 9:50 - 10:10 | Marco Baldovin - Sapienza Università di Roma
Langevin equation in systems with also negative temperatures 
We discuss how to derive a Langevin equation (LE) in non standard systems, i.e. when the kinetic part of the Hamiltonian is not the usual quadratic function. This generalization allows to consider also cases with negative absolute temperature. We first give some phenomenological arguments suggesting the shape of the viscous drift, replacing the usual linear viscous damping, and its relation with the diffusion coefficient modulating the white noise term. As a second step, we implement a procedure to reconstruct the drift and the diffusion term of the LE from the time-series of the momentum of a heavy particle embedded in a large Hamiltonian system. Applying the method to systems with negative temperature, we can observe that also in this case there is a suitable LE, obtained with a precise protocol, able to reproduce in a proper way the statistical features of the slow variables. In other words, even in this context, systems with negative temperature do not show any pathology.
|
| 10:10 - 10:30 | Mattia Radice - Università dell’Insubria
A persistent random walk on an averaged environment for the Lévy-Lorentz gas 
Persistent random walks represent a class of stochastic models where, in their simplest version, a particle jumps to a nearest-neighbour site where there is a probability T of being transmitted and R of being reflected. Such nontrivial, correlated random walks have been recognized as a natural model for a number of relevant settings, from long-chain polymers, to chemotaxis, to active matter, but many of the associated statistical properties still remain unexplored.
We introduce a non-homogeneous, persistent random walk that may be viewed as a mean-field version of the Lévy-Lorentz gas, which consists of an array of scatterers whose distances are distributed according to a Lévy distribution with parameter $0<\alpha<2$, i.e. a distribution whose second moment is not defined. Depending on the values of $\alpha$, the model shows a transition from normal transport ($1<\alpha<2$) to superdiffusion ($0<\alpha<1$), with an exponent $\nu(\alpha)=2/(1+\alpha)$, which is analytically derived by an appropriate continuum limit.
Joint work with Roberto Artuso, Giampaolo Cristadoro and Manuele Onofri
|
| 10:30 - 10:50 | Alessandro Colombo - Università degli Studi di Milano
Miming the Memes for Imaging the Unimagined 
Coherent Diffractive Imaging (CDI) is a technique for imaging matter hit by coherent radiation. The experimentally recorded diffraction pattern $I_{i,j}$ is the square modulus of the Fourier Transform (FT) of the sample density distribution $\rho_{i,j}$, while any information about its phases is lost. Therefore, the inverse FT to get the real-space image of the sample can be accomplished only after the retrieval of the phase information by means of suitable algorithms. These algorithms treats each entry of $\rho_{i,j}$ as a free parameter, trying to optimize the discrepancy with the experimental measurement $I_{i,j}$.
The number of unknowns involved in the optimization, which merely are the pixels of the image $\rho_{i,j}$, runs from $10^5$ for 2D CDI up to $10^7$ for the 3D case. This means that the solution is a point in a $10^{5 \sim 7}$-dimensional space. Standard deterministic algorithms for phase retrieval are iterative gradient-based approaches, which suffer from many limitations, among which stagnation in local optima. On the other side, purely stochastic approaches are doomed to fail, due to the high dimensionality of the optimization problem and the involvement of the Fourier Transform in the evaluation of the cost function.
Our hybrid stochastic method, called Memetic Phase Retrieval (MPR) [1], mixes a genetic algorithm with gradient-based procedures, giving rise to a memetic algorithm, a class of stochastic optimization methods representing one of the recent growing areas of research in evolutionary computation. In particular, MPR treats a population of candidate solutions to the problem, which are able to self-improve via standard iterative approaches, and combines, step by step, their information by the use of computational intelligence. The complex dynamic of MPR is capable to approach and identify the solution much better than the standard procedures. Imaging results on 2D and 3D imaging will be presented, along with a description of the method, showing how much computational intelligence is effective in facing such a complex optimization problem.
[1] Colombo, Alessandro, et al. "Facing the phase problem in coherent diffractive imaging via memetic algorithms." Scientific Reports 7 (2017): 42236.
|
| 10:50 - 11:20 | coffee break |
| 11:20 - 11:40 | Marco Faccioli - Università di Padova
Gaussian fluctuations in quantum phase transitions 
We discuss the effect of Gaussian quantum fluctuations close to the
critical point of a quantum phase transition [1]. In particular, we analyze the
effective action of the Bose-Hubbard Hamiltonian close to the Mott-superfluid
phase transition [2]. This effective action contains the familiar Ginzburg-Landau-Wilson terms [3]
but also first order and second order time derivatives of the complex order parameter.
We investigate the elementary excitations of this effective action finding that they are in
good agreement with experimental data [4]. From the elementary excitations
and using dimensional regularization [5], we determine beyond-mean-field
Gaussian corrections to the zero-temperature equation of state of the system.
We show that these Gaussian corrections crucially depend on the dimensionality of the system.
[1] S. Sachdev, Quantum Phase Transitions (Cambridge Univ. Press, 2012).
[2] K. Sengupta and N. Dupuis, Phys. Rev. A 71, 033629 (2005).
[3] D. Amit, Field Theory, the Renormalization Group and Critical Phenomena (World Scientific, 2005).
[4] M. Endres et al., Nature 487, 454 (2012).
[5] L. Salasnich and F. Toigo, Phys. Rep. 640, 1 (2016).
|
| 11:40 - 12:00 | Francesco Mambretti - Università degli Studi di Milano
Energy-landscape driven crystallization slowdown in supercooled liquid mixtures 
Crystallization is a process of fundamental importance in a variety of fields ranging from materials to climate science. At the microscopic level, crystallization in supercooled liquids is described qualitatively by the classical crystal nucleation and growth theories. In general, however, solid formation is a far more complex process and even the rich behavior observed in simple binary mixtures greatly challenges our current understanding of crystallization. Recently, I joined the group of R. Grisenti in an experimental campaign at DESY, Germany, based on innovative x-ray scattering measurements on liquid microjets [1]. The results have revealed a non-trivial dependence of the crystallization rate on the mixing ratio of supercooled Argon-Krypton liquid mixtures. Our Molecular Dynamics simulations show that this dependence is mainly related to an increased probability for fluctuations between crystal-like and liquid-like states at the crystal/liquid interface driven by the change in the potential energy landscape with composition. The emerging picture might be valid in general, providing a major step towards a more sophisticated theory of crystal growth in out-of-equilibrium supercooled liquids. Moreover, these results support the hypothesis[2] that the energy-landscape complexity may play a leading role also in systems characterized by a higher supercooling degree and by the competition between the crystal formation and the onset of a glassy phase.
1) R.E. Grisenti et al., Phys. Rev. Lett. 90, 234501 (2003)
2) P.G. Debenedetti et al., Nature 410, 259 (2001)
|
| 12:00 - 12:20 | Chahan Kropf - INFN, Pavia
Optimal exciton current in one-dimensional chains 
Finding optimal parameters for exciton transport in small quantum systems is an important step to guide the building of novel and efficient light-harvesting devices. In one-dimensional models of finite size attached to a lead (modeled to study exciton transport) coherence-enhanced transport is achieved when the coupling to the lead is close to the superradiant transition [1].
Using these results we show that such coherence-enhanced transport is compatible with the parameters of transition metal oxides thin films, and thus the latter can potentially be used for experimental verification. In addition, we benchmark our model with more realistic dynamical mean-field theory (DMFT) calculations of a Hubbard model in the Mott insulating phase in a parameter range close to the optimum. Our work suggests that coherence-enhanced transport is achievable in nano-scale solid state devices which would provide an experimental platform for research on light-harvesting devices with substantial advantages over their bio-molecule based counterparts.
1. G.L. Celardo, F. Borgonovi, M. Merkli, V.I. Tsifrinovich, and G.P. Berman, J. Phys. Chem. C, 116, 22105 (2012)
|
| 12:20 - 12:40 | Rosa Giuliano - Università della Calabria
Persistent current and zero-energy Majorana modes in a p-wave disordered superconducting ring 
In this talk will be discussed the emergence of zero-energy Majorana modes in a disordered finite-length p-wave one-dimensional superconducting ring, pierced by a magnetic flux Φ when it is tuned at an appropriate value Φ=Φ∗. In the absence of fermion parity conservation, will be evidenced the emergence of the Majorana modes by looking at the discontinuities in the persistent current I[Φ] at Φ=Φ∗. By monitoring the discontinuities in I[Φ], will be sho9wn how to map out the region in parameter space characterized by the emergence of Majorana modes in the disordered ring.
|
| 12:40 - 13:00 | Andrea Colcelli - SISSA, Trieste
Deviations from Off-Diagonal Long-Range Order and Mesoscopic Condensation in One-Dimensional Quantum Systems 
A quantum system exhibits off-diagonal long-range order (ODLRO) when the largest eigenvalue $\lambda_0$ of the one-body-density matrix scales as $\lambda_0 \sim N$, where $N$ is the total number of particles. Putting $\lambda_0 \sim N^{{\cal C}}$ to define the scaling exponent ${\cal C}$, then ${\cal C}=1$ corresponds to ODLRO and ${\cal C}=0$ to the single-particle occupation of the density matrix orbitals. When $0<{\cal C}<1$, ${\cal C}$ can be used to quantify deviations from ODLRO. In this talk I will present the study of the exponent ${\cal C}$ in a variety of one-dimensional bosonic and anyonic systems.
|
| 13:00 - 14:30 | lunch break |
| 14:30 - 14:50 | Zeno Filiberti - Università degli studi dell'Insubria
A statistical approach to thermo-osmosis 
P. Anzini Z. Filiberti and A. Parola
Fluids in temperature gradients are among the simplest systems out of equilibrium and
serve as testing ground for our understanding of stationary, non equilibrium states.
A temperature gradient in the bulk drives a heat flux, while the local density changes and the pressure remain
uniform, granting mechanical equilibrium. However, near a surface, the pressure balance cannot be
realized and the fluid is set into motion. This phenomenon is known as thermo-osmosis and has been
studied in rarefied gases since many years [1,2]. The same effect is also expected
in liquids, although the lengthscales involved are much shorter.
Arguments based on non equilibrium thermodynamics led Derjaguin to conclude that
the phenomenon originates at the wall-fluid interface and an approximate expression for the
thermo-osmotic velocity in liquids was proposed [3]. Only recently
numerical simulations attempted a quantitative investigation of this effect, while a direct
experimental evidence is still missing. Here, starting from a microscopic model of
molecular fluid and taking advantage of the Kubo-Mori linear response theory, we provide a first principle
description of the phenomenon. By specializing the resulting expressions to the liquid and to the gas regimes we show that
two quite different physical mechanisms are at work: while in dense fluids the phenomenon
originates from the anisotropies of the pressure tensor near the wall, in agreement with Derjaguin
approach, in the rarefied limit the mechanism has a purely kinetic nature and the linear
response formalism confirms the understanding based on kinetic theories.
[1] F.H. Kennard, "Kinetic Theory of Gases" (McGraw Hill, 1938)
[2] Y. Sone, Annu. Rev. Fluid Mech. 32, 779 (2000)
[3] N.V. Churaev, B.V. Derjaguin, V.M. Muller, "Surface Forces" (Springer 1987)
|
| 14:50 - 15:10 | Lorenzo Caprini - Gran Sasso Science Institute (GSSI)
Activity induced delocalization and freezing in self-propelled systems 
We study a system of interacting active particles, propelled by colored noises, characterized by an activity time $\tau$, and confined by a single-well anharmonic potential. We observe that - already with negligible interactions - increasing $\tau$ pushes the particles far from the potential minimum, until a saturation distance is reached. We compute the phase diagram (activity vs interaction length), showing that interaction does not spoil this delocalisation phenomenon but induces a liquid- or solid-like structure in the densest regions. An approximate analytical scheme gives fair predictions for the density profiles in the weakly interacting case. The analysis of non-equilibrium heat fluxes of the system reveals that in the region of largest concentration of particles equilibrium is restored in several aspects.
|
| 15:10 - 15:30 | Francesco De Santis - Sapienza Università di Roma
Computation of the Zero Temperature RSB order parameter in Bethe Lattice Spin Glasses 
Bethe Lattice Spin Glasses are models with finite connectivity which undergo a Replica Symmetry Breaking (RSB) phase transition in field, at zero temperature. We compute numerically the RSB order parameter of the model near the transition, in the case of minimum connectivity (z=3) and bimodal distribution of the couplings (J=±1). The method is based on a universal formula which relates the order parameter to the joint probability distribution of the energy difference and overlap of excitations induced by a convenient perturbation to the Hamiltonian.
|
| 15:30 - 15:50 | Giacomo Rapisardi - Scuola IMT Alti Studi Lucca
Multiple structural transitions in interacting networks 
Many real-world systems can be modeled as interconnected multilayer networks, namely a set of networks interacting with each other. Here we present a perturbative approach to study the properties of a general class of interconnected networks as inter-network interactions are established. We reveal multiple structural transitions for the algebraic connectivity of such systems, between regimes in which each network layer keeps its independent identity or drives diffusive processes over the whole system, thus generalizing previous results reporting a single transition point. Furthermore we show that, at first order in perturbation theory, the growth of the algebraic connectivity of each layer depends only on the degree configuration of the interaction network (projected on the respective Fiedler vector), and not on the actual interaction topology. Our findings can have important implications in the design of robust interconnected networked system, particularly in the presence of network layers whose integrity is more crucial for the functioning of the entire system. We finally show results of perturbation theory applied to the adjacency matrix of the interconnected network, which can be useful to characterize percolation processes on such systems.
|
| 15:50 - 16:10 | Jonathan Fiorentino - Sapienza Università di Roma
Statistics of optimal information flow in ensembles of regulatory motifs 
Genetic regulatory circuits universally cope with different sources of noise that limit their ability to coordinate input and output signals. In many cases, optimal regulatory performance can be thought to correspond to configurations of variables and parameters that maximize the mutual information between inputs and outputs. Since the mid-2000s, such optima have been well characterized in several biologically relevant cases. Here we use methods of statistical field theory to calculate the statistics of the maximal mutual information (the “capacity”) achievable by tuning the input variable only in an ensemble of regulatory motifs, such that a single controller regulates N targets. Assuming (i) sufficiently large N, (ii) quenched random kinetic parameters, and (iii) small noise affecting the input-output channels, we can accurately reproduce numerical simulations both for the mean capacity and for the whole distribution. Our results provide insight into the inherent variability in effectiveness occurring in regulatory systems with heterogeneous kinetic parameters.
|